Suivant: Fonctions de transfert des Niveau supérieur: Représentation mathématique des systèmes Précédent: Systèmes d'ordre n: Table des matières
L'équation différentielle décrivant le système peut-être mise sous
forme d'un système de ![]() équations du premier ordre explicite:
équations du premier ordre explicite:
![]() Le vecteur
Le vecteur
![]() représente l'état du système (par
exemple la position et la vitesse du système) et le vecteur
représente l'état du système (par
exemple la position et la vitesse du système) et le vecteur
![]() représente l'entrée du système.
représente l'entrée du système.
![]() est la solution générale de cette équation.
est la solution générale de cette équation.
![\includegraphics[%
width=1.0\linewidth]{cours-iup51.eps}](img62.png)
L'équation d'état est liée à la fonction de transfert. En effet une équation différentielle d'ordre n est équivalente à un système de n équations différentielles du premier ordre. Donc un système d'ordre n sera représenté par un vecteur d'état de dimension n.
Exemple: prenons le cas d'une masse M soumise à une force f(t).
L'équation différentielle est
![]() . Elle peut
s'écrire comme le système:
. Elle peut
s'écrire comme le système:
On a pris comme variables d'état la position ![]() et la vitesse
et la vitesse
![]() de la masse.
de la masse.
Le système peut s'écrire sous forme matricielle:
donc ici
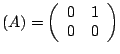 et
et
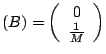
Pierre Moine 2006-02-05