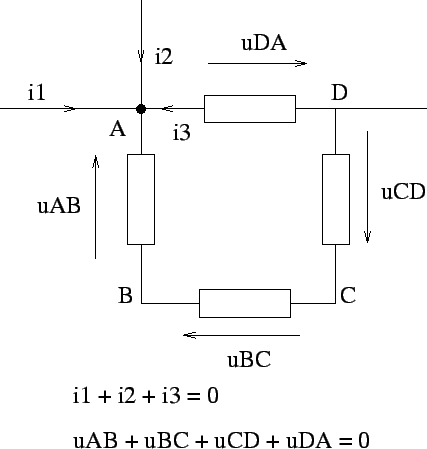
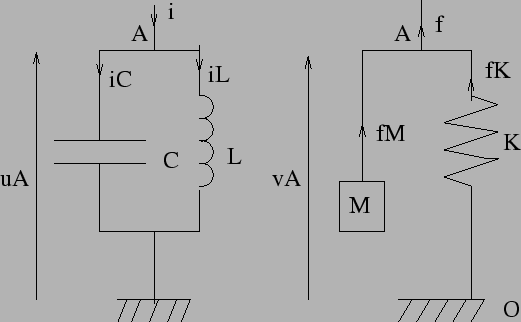
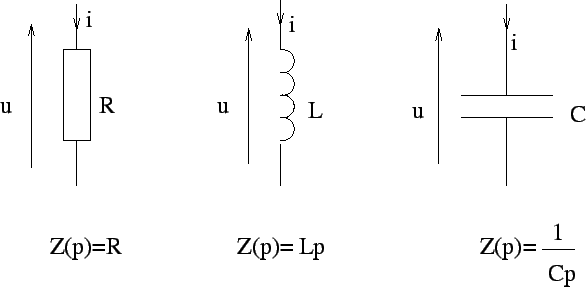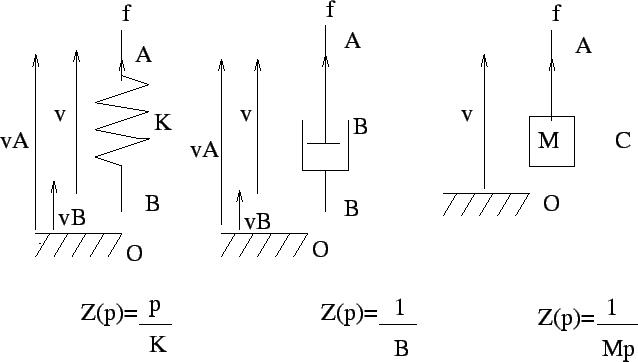Les éléments que nous avons décrits peuvent être représentés sous
forme de dipôles représentés par un rectangle et deux connections
A et B reliant l'élément au reste du système, d'une façon analogue
à la représentation d'une résistance en électricité. On associe à
ce dipôle deux grandeurs conjuguées de telle sorte que le produit
de ces deux grandeurs représente la puissance fournie au dipôle par
le reste du système:
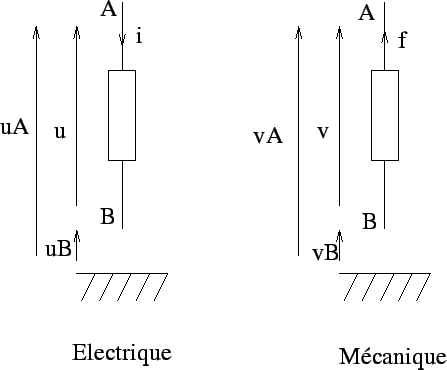
- L'une de ces grandeurs analogue à l'intensité obéit à une loi de conservation:
il s'agit de l'intensité en électricité, qui obéit à la loi des noeuds,
un noeud étant un point équipotentiel (connexion électrique). En mécanique
cette grandeur est la force, le noeud est un point sans masse réalisant
une liaison entre plusieurs éléments mécaniques, en ce point la somme
des forces appliquée est égale à zéro.
- La grandeur conjuguée de la précédente obéit à une loi de composition,
correspondant à la loi de conservation de l'énergie. En électricité
il s'agit de la tension électrique appliquée au dipôle, qui est la
différence de potentiel entre les bornes
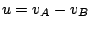 . La loi
des mailles nous montre la composition des tensions: si deux dipôles
sont en série la tension est la somme des deux tensions, ce qui correspond
au fait que la puissance reçue est la somme des puissances reçues
par chaque dipôle:
. La loi
des mailles nous montre la composition des tensions: si deux dipôles
sont en série la tension est la somme des deux tensions, ce qui correspond
au fait que la puissance reçue est la somme des puissances reçues
par chaque dipôle:
En mécanique, la grandeur analogue à la tension est la vitesse, avec
la loi de composition des vitesses. La vitesse du point A par rapport
au point B est la différence des vitesses mesurées par rapport au
référentiel d'inertie: 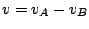 . La puissance mécanique fournie
à l'élément est
. La puissance mécanique fournie
à l'élément est 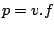
- Impédance généralisée: A partir de cette représentation on peut généraliser
la notion d'impédance:
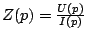 pour les circuits
électriques et
pour les circuits
électriques et
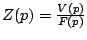 dans l'analogie force-courant.
On peut utiliser les impédances pour remplacer des dipôles en série
ou en parallèle par un dipôle équivalent. Pour des éléments en série
il faut additionner les impédances et pour les éléments en parallèle
il faut additionner les admittances (l'admittance est l'inverse de
l'impédance
dans l'analogie force-courant.
On peut utiliser les impédances pour remplacer des dipôles en série
ou en parallèle par un dipôle équivalent. Pour des éléments en série
il faut additionner les impédances et pour les éléments en parallèle
il faut additionner les admittances (l'admittance est l'inverse de
l'impédance
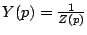 ). Pour un circuit électrique l'impédance
généralisée
). Pour un circuit électrique l'impédance
généralisée 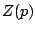 peut se déterminer simplement à partir de l'impédance
complexe habituelle en remplaçant formellement
peut se déterminer simplement à partir de l'impédance
complexe habituelle en remplaçant formellement 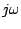 par
par 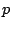 . Attention: lorsqu'on représente une masse l'un des points A ou B
est nécessairement lié au référentiel d'inertie (équivalent à un condensateur
dont une des extrémités est à la masse).
. Attention: lorsqu'on représente une masse l'un des points A ou B
est nécessairement lié au référentiel d'inertie (équivalent à un condensateur
dont une des extrémités est à la masse).
- Exemples:
- Eléments électriques: pour une résistance on a
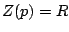 , une inductance
, une inductance
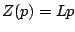 , une capacité
, une capacité
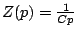
- Eléments mécaniques: pour un amortisseur,
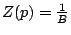 , pour
un ressort,
, pour
un ressort,
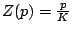 ,
,
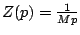
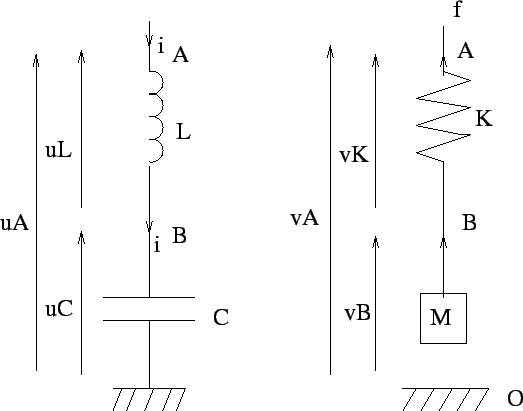
- Eléments en série:
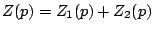
il faut remarquer que la masse étant toujours référencée au référentiel
d'inertie, ne peut être placée en série qu'à l'extrémité d'un assemblage.
Ceci concorde avec le fait que la masse étant ici considérée comme
un point matériel, ne correspond qu'à une seule vitesse et non pas
la composition de deux vitesses comme l'amortisseur ou le ressort.
- Eléments en parallèle:
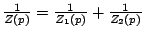
Pierre Moine
2006-02-05